2022年01月24日 力扣每日一题

题目

城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是  绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

  • 例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

  • 你可以 任意次 穿过任意顶点，包括 1 和 n 。
  • 你可以假设在 启程时 ，所有信号灯刚刚变成 绿色 。

 

示例 1：

       

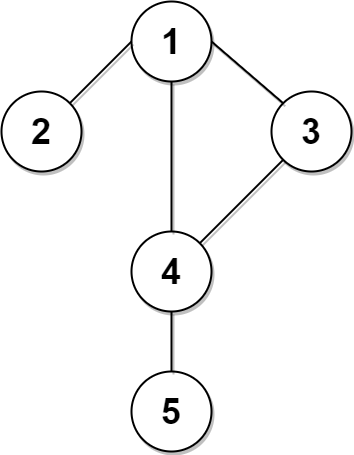
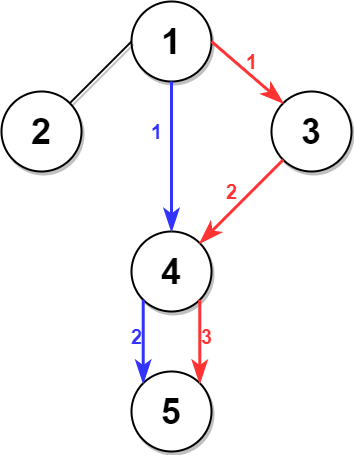
输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

 

提示：

  • 2 <= n <= 104
  • n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • ui != vi
  • 不含重复边
  • 每个节点都可以从其他节点直接或者间接到达
  • 1 <= time, change <= 103
Related Topics
  • 广度优先搜索
  • 图
  • 最短路

    • 个人解法

    {% tabs categories%}

    java
    • 01
    • 02
    • 03
    • 04
    • 05
    • 06
    • 07
    • 08
    • 09
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    import java.util.*;

class Solution {
    public int secondMinimum(int n, int[][] edges, int time, int change) {
        // 统计所有节点的联通节点，并将其存入map中留着后面使用
        Map<Integer, List<Integer>> map = new HashMap<>(n);
        for (int i = 1; i <= n; i++) {
            map.put(i, new ArrayList<>());
        }
        for (int[] edge : edges) {
            map.get(edge[0]).add(edge[1]);
            map.get(edge[1]).add(edge[0]);
        }
        Queue<Integer> queue = new LinkedList<>();
        queue.add(1);
        // 记录节点到达的次数
        int[] counts = new int[n + 1];
        // 记录到达节点的时间
        int free = 0;
        while (!queue.isEmpty()) {
            // 红灯情况下加上需要等待的时间
            if (free % (2 * change) >= change) {
                free += change - free % change;
            }
            free += time;
            // 同一时间可以到达的节点数量
            int size = queue.size();
            // 同一时间节点是否已经到达
            boolean[] use = new boolean[n + 1];
            for (int i = 0; i < size; i++) {
                // 获取该节点接下来可以到达的节点
                List<Integer> list = map.get(queue.poll());
                for (int num : list) {
                    // 同一时间未到达，并且到达该节点的总次数小于2
                    if (!use[num] && counts[num] < 2) {
                        queue.add(num);
                        use[num] = true;
                        counts[num]++;
                    }
                    // 如果是第二次到达最后一个节点，直接返回需要到达的诗句
                    if (num == n && counts[num] == 2) {
                        return free;
                    }
                }
            }
        }
        return 0;
    }
}
    python
    • 01
    • 02
    • 03
    • 04
    • 05
    • 06
    • 07
    • 08
    • 09
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    from collections import deque
from typing import List


class Solution:
    def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:
        # 统计所有节点的联通节点，并将其存入map中留着后面使用
        maps = [[0] for _ in range(n + 1)]
        for edge in edges:
            maps[edge[0]].append(edge[1])
            maps[edge[1]].append(edge[0])
        queue = deque()
        queue.append(1)
        # 记录节点到达的次数
        counts = [0] * (n + 1)
        # 记录到达节点的时间
        free = 0
        while len(queue):
            # 红灯情况下加上需要等待的时间
            if free % (2 * change) >= change:
                free += change - free % change
            free += time
            # 同一时间可以到达的节点数量
            size = len(queue)
            # 同一时间节点是否已经到达
            use = [False] * (n + 1)
            for i in range(size):
                for num in maps[queue.popleft()]:
                    # 同一时间未到达，并且到达该节点的总次数小于2
                    if use[num] is False and counts[num] < 2:
                        queue.append(num)
                        use[num] = True
                        counts[num] += 1

                    # 如果是第二次到达最后一个节点，直接返回需要到达的诗句
                    if num == n and counts[num] == 2:
                        return free
        return 0

    {% endtabs %}