2022年02月12日 力扣每日一题
题目
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
示例 1:
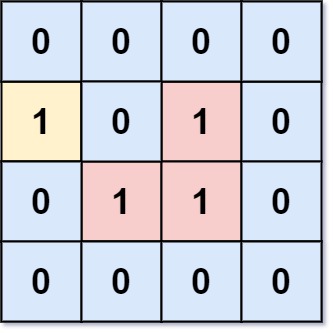
输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] 输出:3 解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
示例 2:
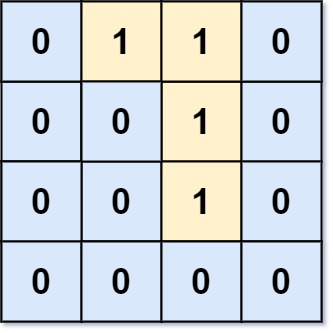
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] 输出:0 解释:所有 1 都在边界上或可以到达边界。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 500grid[i][j]的值为0或1
Related Topics
个人解法
解题方法:广度优先算法
这道题是统计无法力扣网络边界的陆地单元格数量,我的思路是反过来统计,用总陆地数量-能离开的陆地数量
这样的话,我就可以用广度优先算法来进行解决,步骤如下:
- 将边界的单元格坐标加入到队列,并计数
- 依次从队列中取出
- 将取出陆地的相邻陆地加入到队列中,并计数
- 当队列为空时,遍历数组获取总陆地数,并减去能离开的陆地数量
{% tabs categories%}
import java.util.LinkedList;
import java.util.Queue;
class Solution {
public int numEnclaves(int[][] grid) {
boolean[][] use = new boolean[grid.length][grid[0].length];
Queue<int[]> queue = new LinkedList<>();
int xl = grid.length;
int yl = grid[0].length;
int count = 0;
for (int i = 0; i < xl; i++) {
if (grid[i][0] == 1) {
queue.add(new int[]{i, 0});
use[i][0] = true;
count++;
}
if (grid[i][yl - 1] == 1 && !use[i][yl - 1]) {
queue.add(new int[]{i, yl - 1});
use[i][yl - 1] = true;
count++;
}
}
for (int i = 1; i < yl - 1; i++) {
if (grid[0][i] == 1 && !use[0][i]) {
queue.add(new int[]{0, i});
use[0][i] = true;
count++;
}
if (grid[xl - 1][i] == 1 && !use[xl - 1][i]) {
queue.add(new int[]{xl - 1, i});
use[xl - 1][i] = true;
count++;
}
}
int[] xp = new int[]{1, -1, 0, 0};
int[] yp = new int[]{0, 0, 1, -1};
while (!queue.isEmpty()) {
int[] arr = queue.poll();
int x = arr[0];
int y = arr[1];
for (int k = 0; k < 4; k++) {
int nx = x + xp[k];
int ny = y + yp[k];
if (nx >= 0 && nx < grid.length && ny >= 0 && ny < grid[0].length && grid[nx][ny] == 1 && !use[nx][ny]) {
queue.add(new int[]{nx, ny});
use[nx][ny] = true;
count++;
}
}
}
int sum = 0;
for (int[] ints : grid) {
for (int j = 0; j < yl; j++) {
if (ints[j] == 1) {
sum++;
}
}
}
return sum - count;
}
}
from collections import deque
from typing import List
class Solution:
def numEnclaves(self, grid: List[List[int]]) -> int:
use = [[False] * len(grid[0]) for _ in range(len(grid))]
queue = deque()
xl = len(grid)
yl = len(grid[0])
count = 0
for i in range(xl):
if grid[i][0] == 1:
queue.append((i, 0))
use[i][0] = True
count += 1
if grid[i][yl - 1] == 1 and not use[i][yl - 1]:
queue.append((i, yl - 1))
use[i][yl - 1] = True
count += 1
for i in range(1, yl - 1):
if grid[0][i] == 1 and not use[0][i]:
queue.append((0, i))
use[0][i] = True
count += 1
if grid[xl - 1][i] == 1 and not use[xl - 1][i]:
queue.append((xl - 1, i))
use[xl - 1][i] = True
count += 1
while queue:
x, y = queue.pop()
for nx, ny in ((x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)):
if nx < 0 or nx >= len(grid) or ny < 0 or ny >= len(grid[0]) or grid[nx][ny] == 0 or use[nx][ny]:
continue
queue.append((nx, ny))
use[nx][ny] = True
count += 1
sc = sum([sum(row) for row in grid])
return sc - count
{% endtabs %}
